Manipulable embeddings

Vector embeddings are fascinating byproducts of neural networks–parameters that the network learns during training on a particular task.

They've been incredibly useful to me in various applications, from clustering real estate listings to categorising financial expenditures and even analysing baby names.

However, there's a catch

😱 Embeddings convey only intrinsic meaning.

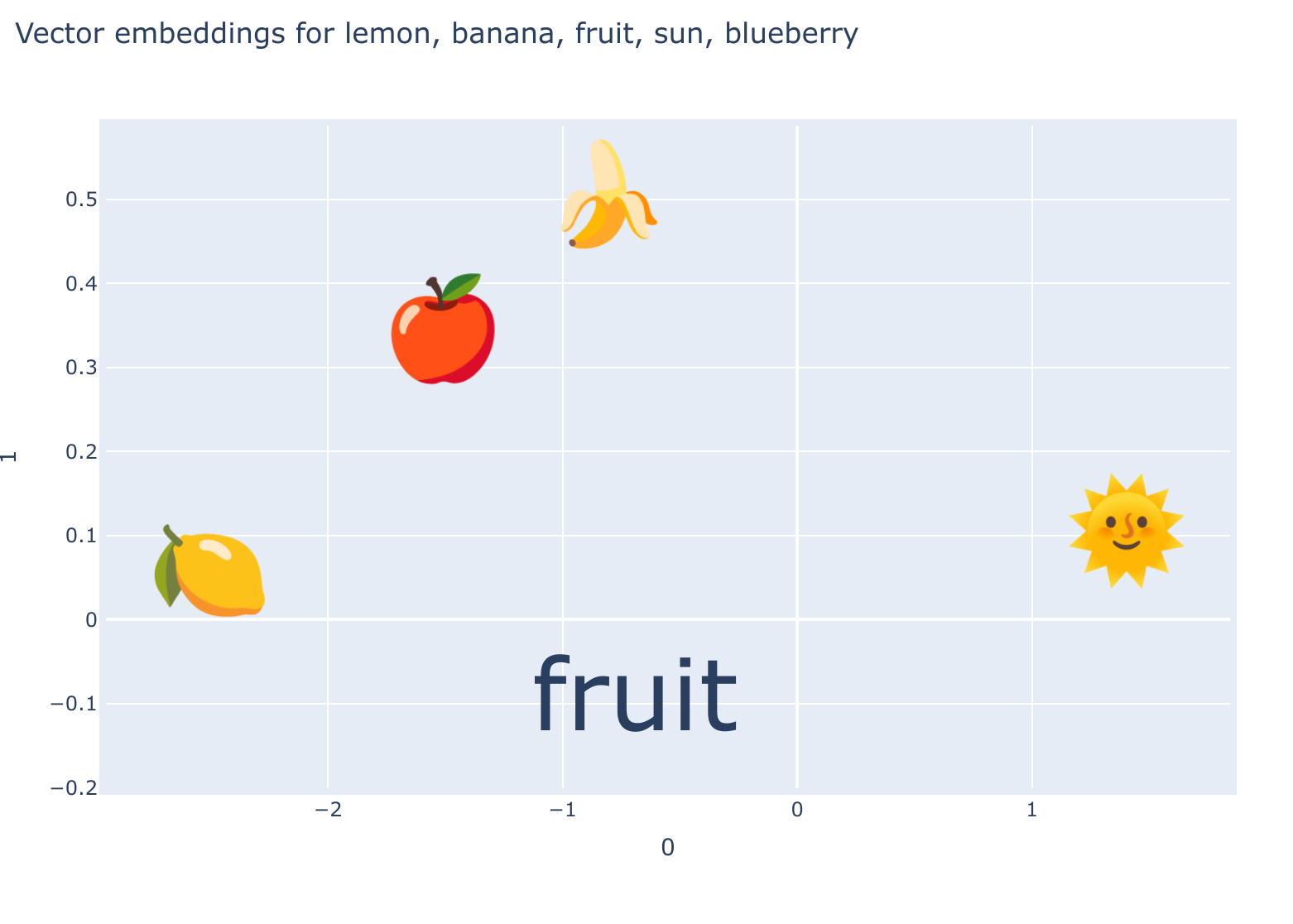
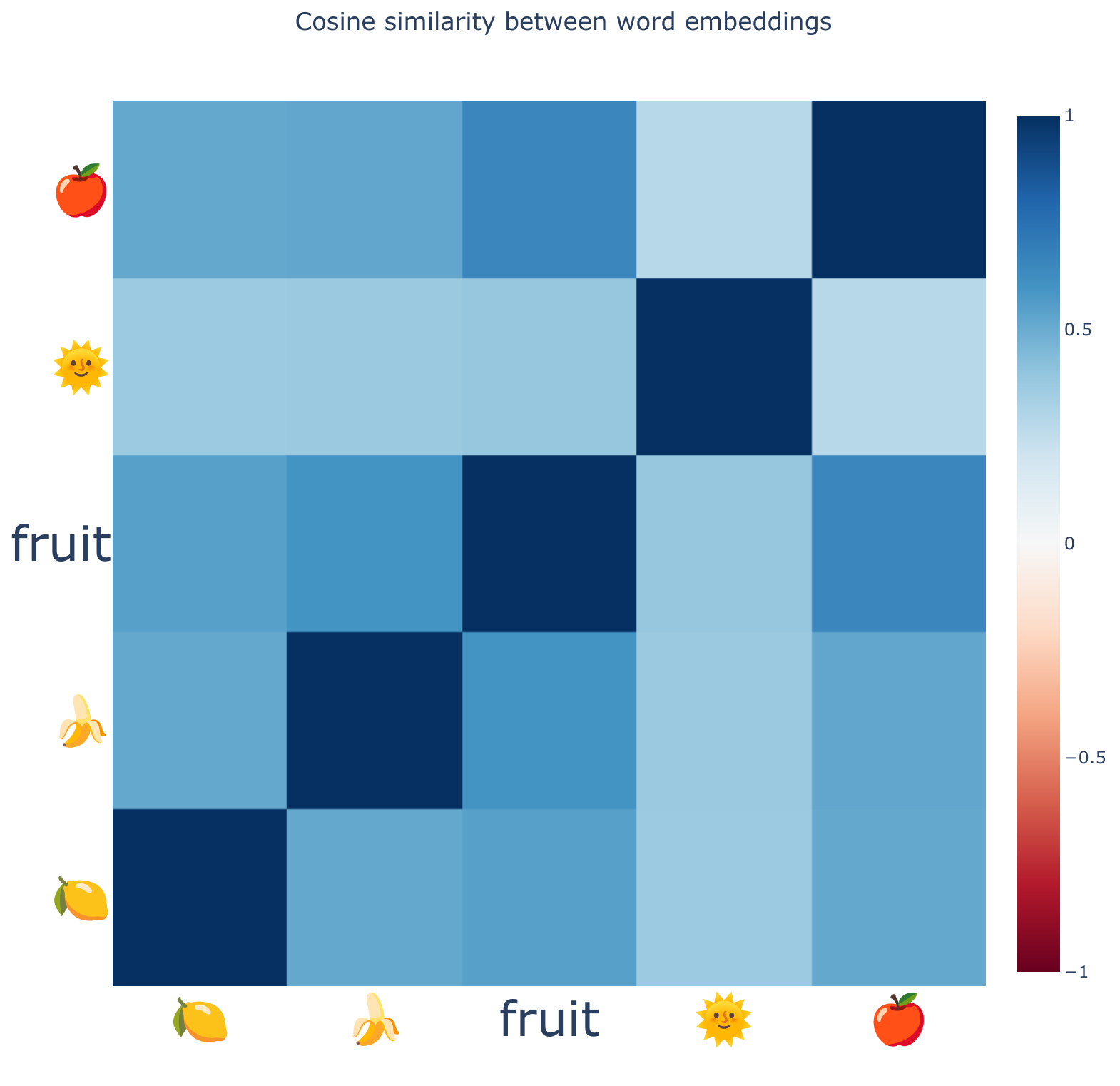
When we transform data into vector embeddings, we receive high-dimensional output data in return, which we often reduce to three dimensions for visualization.

Yet, if we encode words like "banana" and "lemon" into an embedding space, we can't simply tweak their positions to emphasise qualities like "yellowness" or "sweetness", without adding additional context—we might envision "fruit" positioned somewhere in between.

So embeddings are not semantically versatile; they are not intended to encapsulate meaning unrelated to the data.

This limitation makes sense because embeddings are the effect of learning to minimise a loss function that is specific to their training data and prediction tasks—usually natural language processing.

Method for manipulating embeddings by recursive encode-reduce transformation

I've been working on a method to manipulate embeddings by transforming them in an iterative sequence of aggregation, weighting and dimensional reduction.

Here is a very complicated way of saying something very simple, let:

• \(E_i\) be the vector embedding for the (i)-th input.
• \(w_i\) be the weight (coefficient) assigned to the (i)-th embedding.
• \(R(\cdot)\) represent the dimensional reduction operation (e.g., PACMAP).
• \(\oplus\) denote the concatenation operation.
• \(\circ\) represent element-wise multiplication (weighting).

The process can be expressed as a sequence of operations:

Concatenation and Weighting:
\[X_1 = \sum_{i=1}^{n} w_i \cdot E_i\]
Where (X_1) is the weighted sum of the embeddings.

Dimensional Reduction:
\[X_2 = R(X_1)\]
Where \(X_2\) is the result of applying the dimensional reduction operation to \(X_1\).

Repeat Concatenation and Weighting:
\[X_3 = \sum_{i=1}^{n} w_i \cdot X_2\]
Where \(X_3\) is the weighted sum of the vectors obtained from the previous step.

Repeat Dimensional Reduction:
\[X_4 = R(X_3)\]
Where \(X_4\) is the result of applying the dimensional reduction operation to \(X_3\).

Validation