Reverse engineering a soil calculator using symbolic regression


The Elke Haege soil simulator
This post is based on the work of Elke Haege Thorvaldson and Simon Leake (https://www.google.com/search?q=elkeh.com.au and SESL Australia). Elke Haege Thorvaldson is the owner of the calculator, and is an award-winning landscape architect and consulting arborist. The soil calculator, also known as the Soil Volume Simulator (SVS), was a collaborative effort between her and Simon Leake, a soil scientist from SESL Australia
Improving the calculator with continuous variables
This fantastic simulator generates soil volume requirements for trees based on their "designed size". The simulator includes surrounding soil, shared root zones, climatic conditions, maintenance, etc.
Strangely, discrete categories are used for things that have real measurements:

A number of interesting things can be done to improve it:
- Increase precision by using continuous inputs instead of discrete ones
- Find alternative ways to achieve required soil volumes by allowing some variables to be "driven" by others that are fixed and unchangeable.
- Discover trade-offs among factors that can be combined to reduce time/cost to achieve required soil volume
- Discover the key factors contributing to the volumes; what mattered the most?
- Use symbolic regression to derive a simpler equation that could be easier to remember and apply from memory.
- Develop a new interface that is more fluid and fun to use.

How I reverse engineered the simulator
The first task was to get tabular data from the calculator by inputting all possible combinations.
What didn't work:
- Browser automation to click all combinations of inputs using puppeteer to compile a csv
- Duplicating the Wordpress plugin and environment locally to examine its construction.
- Asking GPT-4 to produce an equation using all the factors
Apart from basic operators + - × that calculate answers to values input through drop-downs, there are sets of numbers conditional upon the initial Tree Design Size and Height input.
Since there are between 3 and 5 choices across 8 inputs multiplied by the four Tree Design Size and Height options available, the Cartesian product yields 23,040 combinations of inputs to get all possible soil volumes.
I felt that underneath this calculator, there were more interesting things to discover:
- Are there trade-offs between some factors that could shortlist an optimal set of candidates combinations?
- What were the main factors contributing to the volumes? what mattered the least?
- How to lock some factors and let others be driving?
- Could I train a machine learning model to predict soil volumes allowing any range of continuous variables unconstrained by the current options.
Examining the source code revealed 34 "elements" in an obscure data structure used by the Wordpress plugin.
Using LLMs to reverse engineer formulas is a novel idea which doesn't always work, but sometimes it did:
With some prompting and manual effort, I was able to intuit my way to several correct equations.
However, almost all inputs were mapped to discrete categorical variables in a way that further obscured the underlying equations
The values for Tree Design Size and Height are scaled away from empirical values (eg: small to 4m = 6.0; small/medium 4-9m high = 10.0)
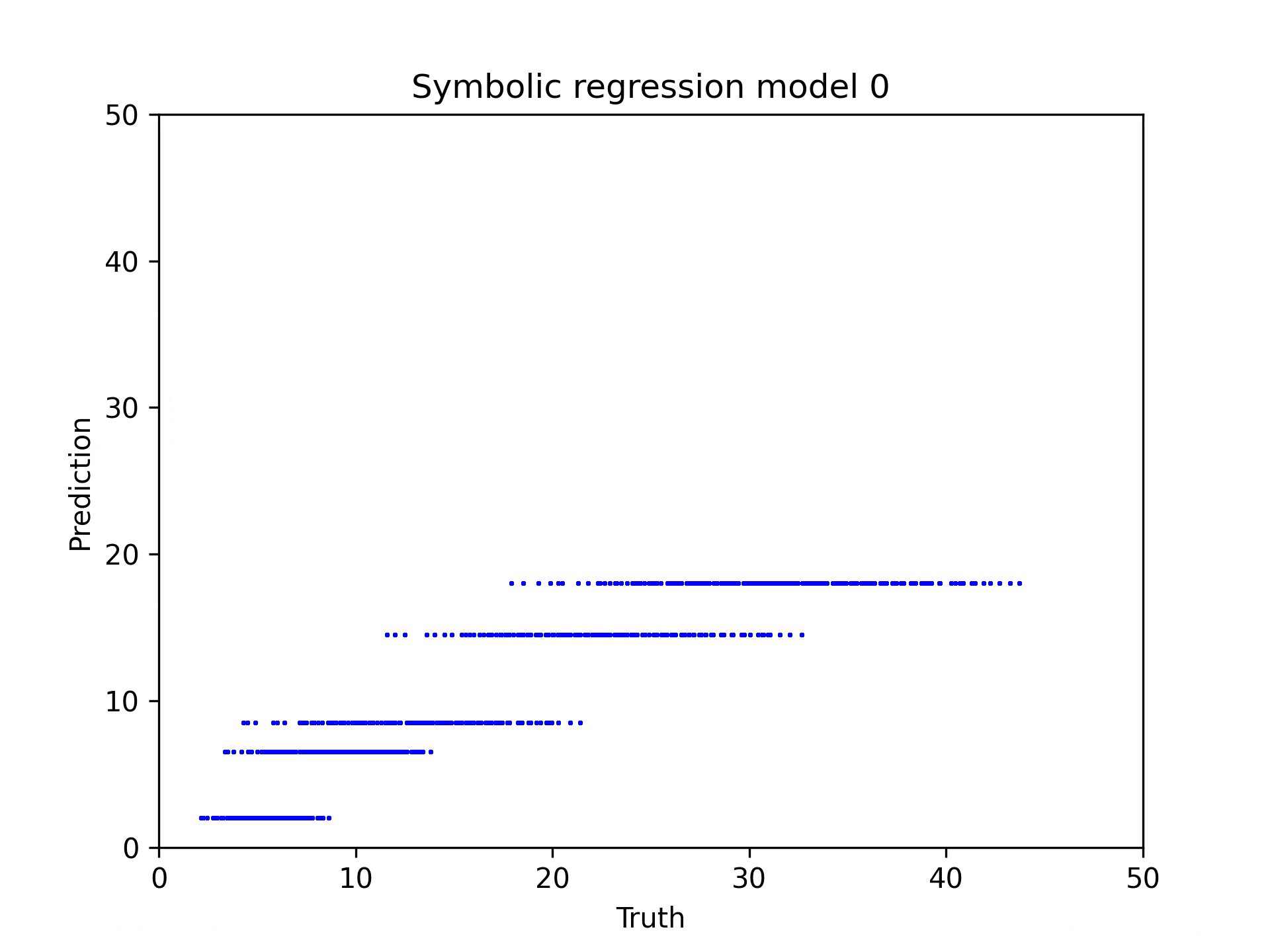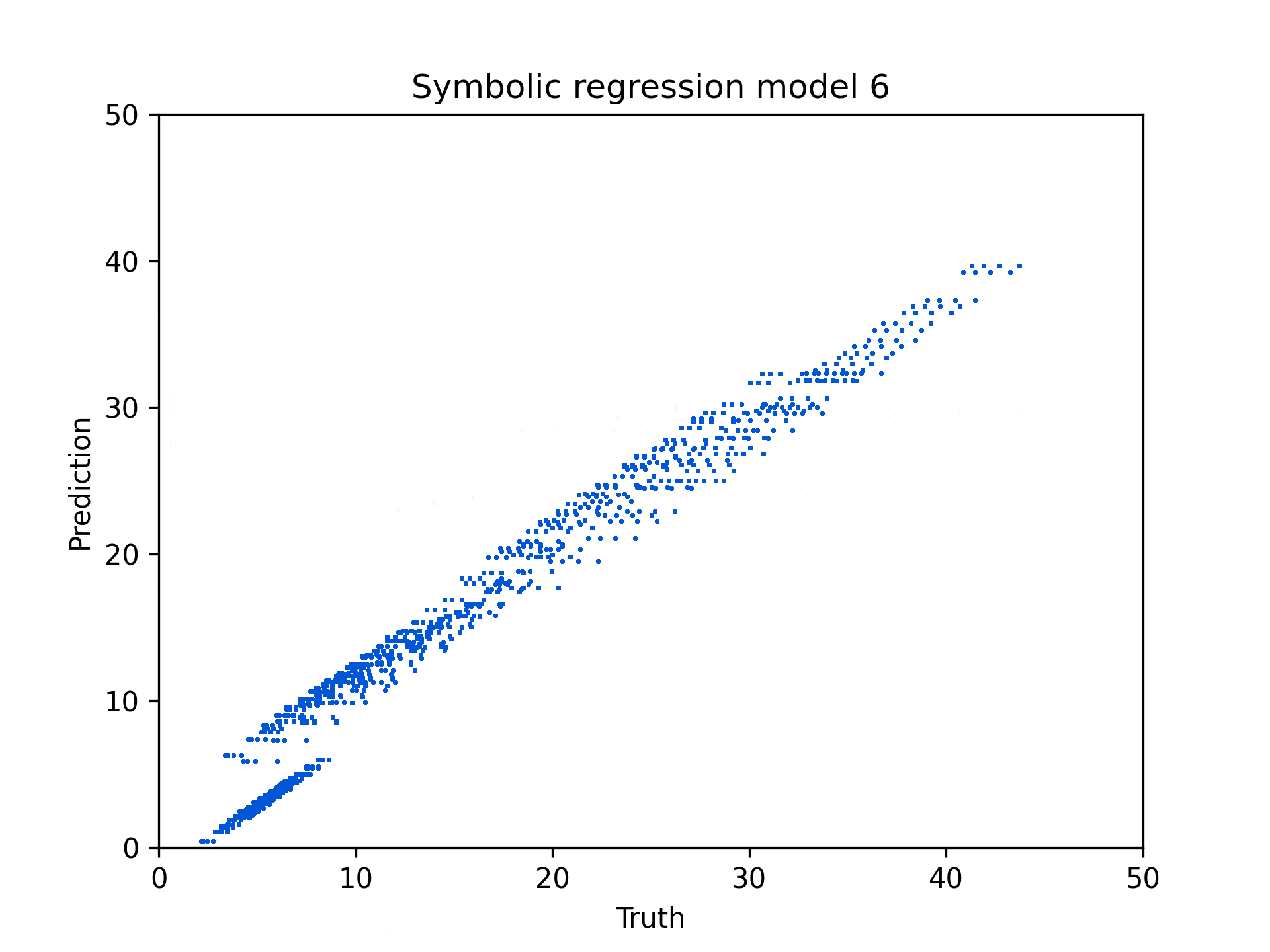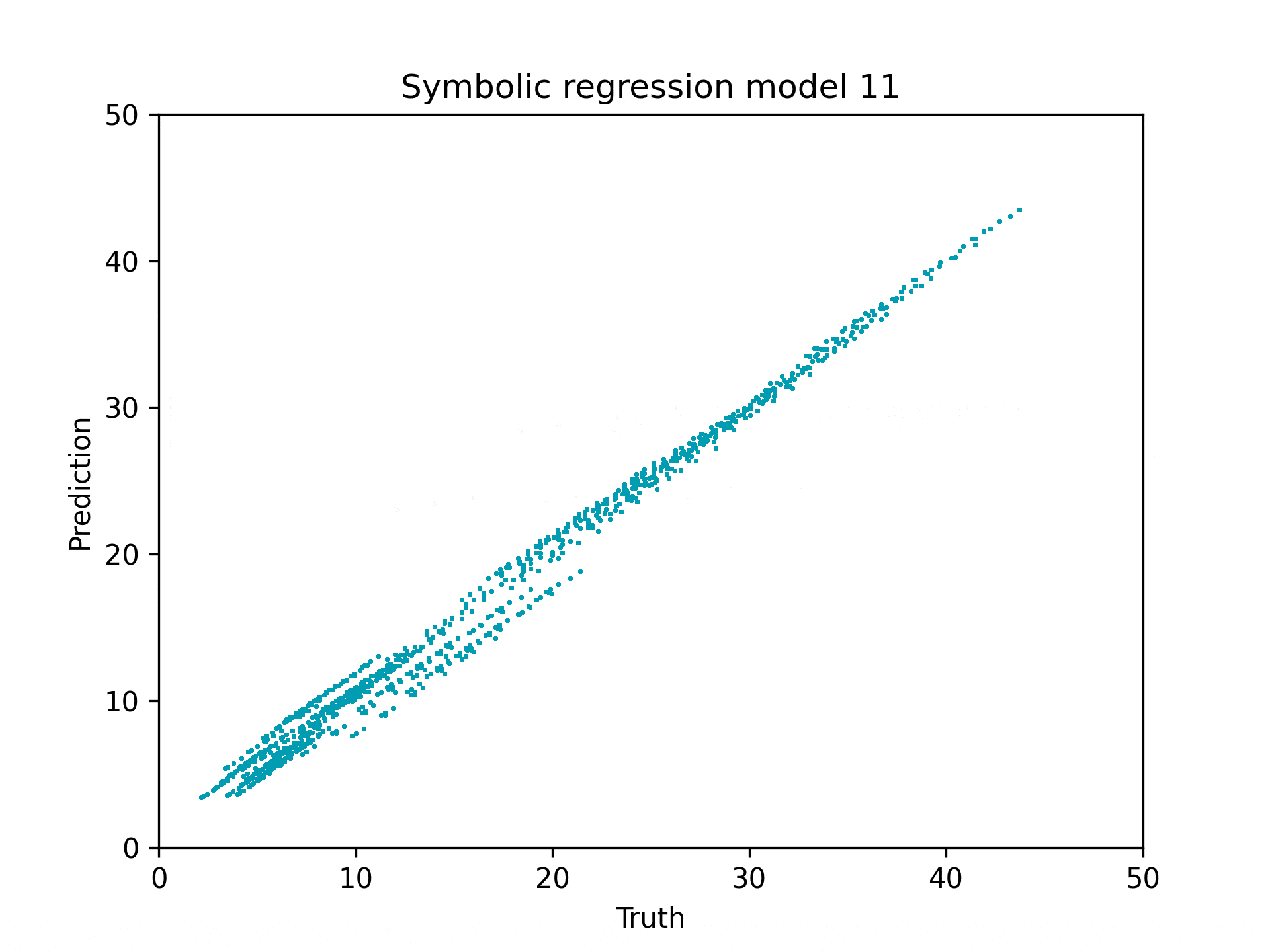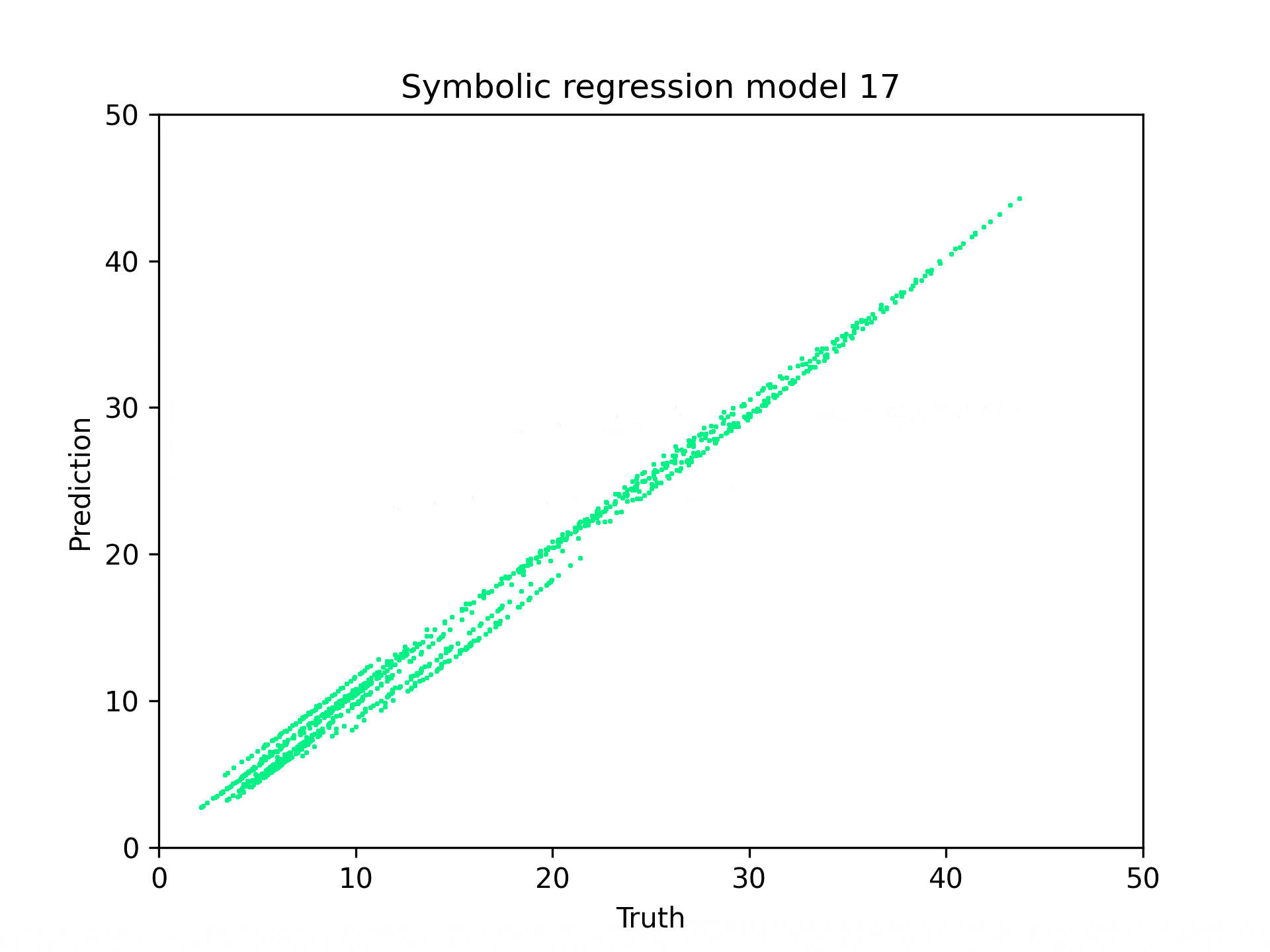
In my symbolic regression analysis of the tree soil calculator, I discovered that while the original interface used discrete categories, the underlying math revealed continuous relationships between variables. Using PySR (Symbolic Regression), I identified that tree height is the dominant predictor of soil volume requirements, with a near-linear relationship (\(y₁ = 1.6387 * text{tree_height}\)) for total soil volume. For tree pit volume specifically, the algorithm uncovered a more complex formula incorporating soil suitability, maintenance factors, and planting replacement time, but still primarily driven by tree height. The percentage of soil volume outside the tree pit inversely affects the tree pit volume requirement, acting as a key modifying factor.
These equations demonstrate why the calculator could be improved by accepting continuous measurements rather than discrete categories. By extracting these mathematical relationships, I've created a more flexible model that allows for precise calculations with any input values, eliminating the constraints of the original categorical approach while preserving the essential relationships between variables.
Symbolic Regression with PySR